You [Gerald Bauer¹] have been permanently banned [for life] from participating in r/ruby (because of your writing off / outside of r/ruby). I do not see your participation adding anything to this [ruby] community.

-- Richard Schneeman (r/ruby mod and fanatic illiberal ultra leftie on a cancel culture mission)

¹: I know. Who cares? Who is this Gerald Bauer anyway. A random nobody for sure. It just happens that I am the admin among other things of Planet Ruby.

Case Studies of Code of Conduct "Cancel Culture" Out-Of-Control Power Abuse - Ruby - A Call for Tolerance On Ruby-Talk Results In Ban On Reddit Ruby

Update (August, 2022) - A Call for More Tolerance And Call For No-Ban Policy Results In Ban On Ruby-Talk (With No Reason Given) 

>  I just banned gerald.bauer@gmail.com.
>
>  -- SHIBATA Hiroshi
>
>> THANK YOU
>> 
>>  -- Ryan Davis
>>
>>
>> My full support to moderators.
>>
>> -- Xavier Noria
>> 
>> My full support to moderators.
>>
>>  -- Carlo E. Prelz
>>
>>  That's fun.
>>
>>  -- Alice

Read the full story »

« Ruby Blockchain Week 2021, January 3rd to January 9th - 7 Days of Ruby (Crypto) Gems

Day 5 - elliptic Gem - Open Up 10,000,000,000 Accounts - Bank the Unbanked Using Elliptic Curve (EC) Cryptography and the Digital Signature Algorithm (DSA) - Be Your Own Bank

Written by geraldb Gerald Bauer

A code monkey formerly at Big Korupto. Jobless no coiner having fun staying poor and wrong. Writing the Get Rich Quick “Business Blockchain” Bible - The Secrets of Free Easy Money.

Let’s start with a trivia quiz.

Q: How long does it take to open up 10 000 (bank) accounts?

Did you know? All you need to open up a new account on a blockchain is an (unsigned) 256-bit / 32 byte integer number. Yes, that’s it. No questions asked. The private key is the secret “magic” that unlocks your own bank.

Remember: NEVER share your private keys! Not your keys, not your money!

If your crypto is stored in an online wallet you don’t have the private keys for (like a wallet on an exchange), is it really yours? Many will say hacks happen.

Let’s continue with another trivia quiz:

Q: What’s the maximum value for a 256-bit / 32 byte integer number (hint 2^256-1)?

Maximum value of 2^256-1 =

2**256-1
#=> 115792089237316195423570985008687907853269984665640564039457584007913129639935
(2**256-1).to_s.length
#=> 78

Yes, that’s 78 (!) decimal digits.

Let’s (re)try the maximum value for a 256-bit (32 byte) integer number in hexadecimal (base 16) and binary (base 2) format?

(2**256-1).to_s(16)
#=> "ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff"
(2**256-1).to_s(16).length
#=> 64

(2**256-1).to_s(2)
#=> "1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111"
(2**256-1).to_s(2).length
#=> 256

Surprise - a 256-bit number has 256 binary digits (0 and 1s).

BEWARE - Blockchain Bandits! If you use a low integer number e.g. 1, 2, etc. your account is guaranteed to get robbed by blockchain bandits in seconds.

(See A “Blockchain Bandit” Is Guessing Private Keys and Scoring Millions by Andy Greenberg, Wired Magazine, April 2019)

If you ask - How big (or how safe) is a (random) 256-bit / 32 byte integer number?

Yes, 256-bit is that big - there aren’t enough atoms in the universe.

Bitcoin Trivia:

As initially the sole and subsequently the predominant miner, Satoshi Nakamoto [the pseudonymous Bitcoin founder] was awarded bitcoin at genesis and for 10 days afterwards. Except for test transactions these remain unspent since mid January 2009. The public bitcoin transaction log shows that Nakamoto’s known addresses contain roughly one million bitcoins. At bitcoin’s peak in December 2017, this was worth over US$19 billion, making Nakamoto possibly the 44th richest person in the world at the time.

(Source: Satoshi Nakamoto @ Wikipedia)

The one million bitcoins are yours if the pay-to-pubkey (p2pk) script returns with true. The only input you need to unlock the fortune is the private key. Are you Satoshi?

Auto-Generate/Calculate the Public Key - Enter Elliptic Curve (EC) Cryptography

An ECDSA (Elliptic Curve Digital Signature Algorithm) private key is a random number between 1 and the order of the elliptic curve group. The public key are two numbers (that is, a point with the coordinates x and y) computed by multiplying the generator point (G) of the curve with the private key. This is equivalent to adding the generator to itself private_key times. Magic? Let’s try:

require 'elliptic'

# This private key is just an example. It should be much more secure!
private_key = EC::PrivateKey.new( 1234 )   # by default uses Secp256k1 curve (used in Bitcoin and Ethereum)

public_key =  private_key.public_key   ## the "magic" one-way K=k*G curve multiplication (K=public key,k=private key, G=generator point)
point = public_key.point

point.x
#=> 102884003323827292915668239759940053105992008087520207150474896054185180420338
point.y
#=> 49384988101491619794462775601349526588349137780292274540231125201115197157452

point.x.to_s(16)
#=> "e37648435c60dcd181b3d41d50857ba5b5abebe279429aa76558f6653f1658f2"
point.y.to_s(16)
#=> "6d2ee9a82d4158f164ae653e9c6fa7f982ed8c94347fc05c2d068ff1d38b304c"

And to get the all-in-one-string public key from a point with the coordinates x and y use the 1) uncompressed format or the 2) compressed format:

# 1) Uncompressed format (with prefix 04)
#   Convert to 64 hexstring characters (32 bytes) in length

prefix = '04'
pubkey = prefix + "%064x" % point.x + "%064x" % point.y
#=> "04e37648435c60dcd181b3d41d50857ba5b5abebe279429aa76558f6653f1658f26d2ee9a82d4158f164ae653e9c6fa7f982ed8c94347fc05c2d068ff1d38b304c"

# 2) Compressed format (with prefix - 02 = even / 03 = odd)
#   Instead of using both x and y coordinates,
#   just use the x-coordinate and whether y is even/odd

prefix = point.y % 2 == 0 ? '02' : '03'
pubkey = prefix + "%064x" % point.x
#=> "02e37648435c60dcd181b3d41d50857ba5b5abebe279429aa76558f6653f1658f2"

That’s all the magic.

Aside - Elliptic What?

Elliptic-curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields.

(Source: Elliptic-curve cryptography @ Wikipedia)

What’s an Elliptic Curve?

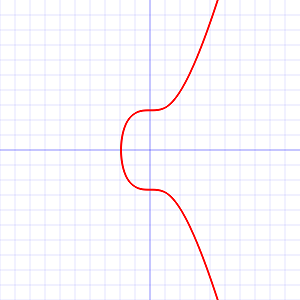
This is a graph of secp256k1’s elliptic curve y² = x³ + 7 over the real numbers. Note that because secp256k1 is actually defined over the field Zₚ, its graph will in reality look like random scattered points, not anything like this.

(Source: Secp256k1 @ Bitcoin Wiki)

Sign & Verify Transactions

Sign a transaction with an (elliptic curve) private key:

# Step 1 - Calculate the Transaction (tx) Hash
tx = 'from: Alice  to: Bob     cryptos: 43_000_000_000'
txhash = Digest::SHA256.digest( tx )

# Step 2 - Get the Signer's Private key
private_key = EC::PrivateKey.new( 1234 )     # This private key is just an example. It should be much more secure!

# Sign!
signature = private_key.sign( txhash )
# -or-
signature = EC.sign( txhash, private_key )

signature.r
#=> 80563021554295584320113598933963644829902821722081604563031030942154621916407
signature.s
#=> 58316177618967642068351252425530175807242657664855230973164972803783751708604

signature.r.to_s(16)
#=> "3306a2f81ad2b2f62ebe0faec129545bc772babe1ca5e70f6e56556b406464c0"
signature.s.to_s(16)
#=> "4fe202bb0835758f514cd4a0787986f8f6bf303df629dc98c5b1a438a426f49a"

Verify a signed transaction with an (elliptic curve) public key:

# Step 1 - Calculate the Transaction (tx) Hash
tx = 'from: Alice  to: Bob     cryptos: 43_000_000_000'
txhash = Digest::SHA256.digest( tx )

# Step 2 - Get the Signer's Public Key
public_key = EC::PublicKey.new(
   102884003323827292915668239759940053105992008087520207150474896054185180420338,
   49384988101491619794462775601349526588349137780292274540231125201115197157452
)

# Step 3 - Get the Transaction's Signature
signature = EC::Signature.new(
  80563021554295584320113598933963644829902821722081604563031030942154621916407,
  58316177618967642068351252425530175807242657664855230973164972803783751708604
)

# Don't Trust - Verify
public_key.verify?( txhash, signature )
# -or-
EC.verify?( txhash, signature, public_key )
#=> true


# or using hexadecimal numbers

public_key = EC::PublicKey.new(
  0xe37648435c60dcd181b3d41d50857ba5b5abebe279429aa76558f6653f1658f2,
  0x6d2ee9a82d4158f164ae653e9c6fa7f982ed8c94347fc05c2d068ff1d38b304c
)

signature = EC::Signature.new(
  0x3306a2f81ad2b2f62ebe0faec129545bc772babe1ca5e70f6e56556b406464c0,
  0x4fe202bb0835758f514cd4a0787986f8f6bf303df629dc98c5b1a438a426f49a
)

public_key.verify?( txhash, signature )
# -or-
EC.verify?( txhash, signature, public_key )
#=> true

Find Out More

References

Built with Ruby (running Jekyll) on 2023-01-25 18:05:39 +0000 in 0.371 seconds.
Hosted on GitHub Pages. </> Source on GitHub. (0) Dedicated to the public domain.